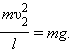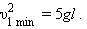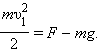| Главная » Файлы » Дистанционное обучение » Системный администратор 1 курс |
| 20.10.2020, 15:57 | |||||||||||||||||||||||||||||||
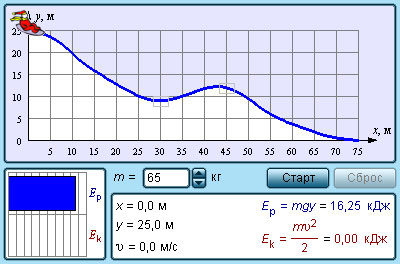
"Энергия. Кинетическая энергия. Потенциальная энергия. Закон сохранения механической энергии. Применение законов сохранения" Кинетическая и потенциальная энергииЕсли тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась, то силы совершили определенную работу A. Работа всех приложенных сил равна работе равнодействующей силы.
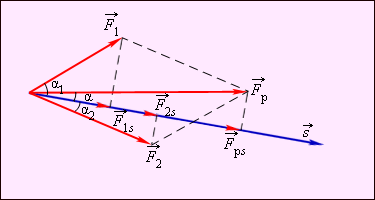
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы. В этом случае векторы силы, перемещения, скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
Отсюда следует, что
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости). Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью, равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью, то для его полной остановки необходимо совершить работу
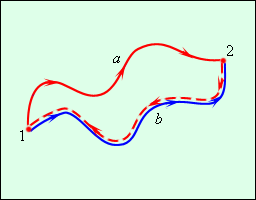
В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел. Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю. Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести
Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY, направленную вертикально вверх:
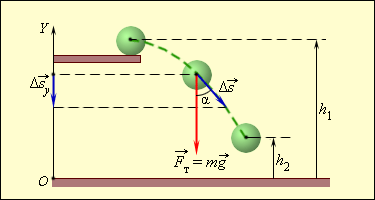
где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY (рис. 1.19.3), то сила тяжести совершила работу
Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Потенциальная энергия Eр зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
где M – масса Земли, G – гравитационная постоянная. Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости. Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя. Закон сохранения механической энергииЕсли тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Следовательно
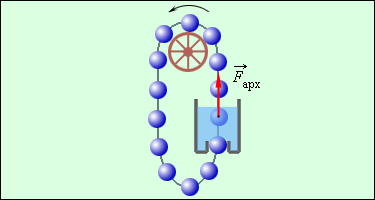
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии. Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Рисунок ниже поясняет решение этой задачи.
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
Из этих соотношений следует:
Центростремительное ускорение в нижней точке создается силами направленными в противоположные стороны:
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
Прочность нити должна, очевидно, превышать это значение. Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач. В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды. Сила трения не является консервативной. Работа силы трения зависит от длины пути. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии. Дополнительные источники: - Опыт на Закон сохранение энергии: https://www.youtube.com/watch?v=8lAlSHb-C5o&feature=emb_logo&ab_channel=GalileoRU - Онлайн объяснение: https://resh.edu.ru/subject/lesson/6290/main/197457/ - Простая наука это интересно: https://www.youtube.com/watch?v=vkkNCmXHUr0&feature=emb_logo&ab_channel=%D0%9D%D0%B0%D1%83%D0%BA%D0%B02.0 Домашнее задание: 1. Сделать краткий конспект темы в тетради, выделить основные понятия, определения, формулы и законы (предоставлять фотографии конспекта не нужно). 2. Проделать самостоятельно любой опыт на тему "Закон сохранения энергии" и объяснить его. Объяснение и фотографии проделанного опыта предоставить в отчете о проделанной работе на электронный адрес. 3. Задачи для закрепления полученных знаний: - Пуля массой 20 г выпущена под углом 600 к горизонту с начальной скоростью 600 м/с. Определите кинетическую энергию пули в момент наивысшего подъема. - Пружина удерживает дверь. Для того чтобы приоткрыть дверь, растянув пружину на 3 см, нужно приложить силу равную 60 Н. Для того, чтобы открыть дверь, нужно растянуть пружину на 8 см. Какую работу необходимо совершить, чтобы открыть закрытую дверь? - Камень брошен с поверхности Земли вертикально вверх со скоростью 10 м/с. На какой высоте кинетическая энергия камня уменьшится в 5 раз по сравнению с начальной кинетической энергией. Отправляете фото или Word-файл на электронный адрес lenr89@mail.ru, не забываем подписать группу и ФИО. | |||||||||||||||||||||||||||||||
| Просмотров: 52 | Загрузок: 0 | | |||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
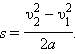
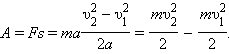
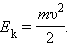
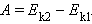
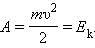
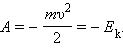
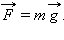
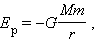
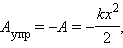
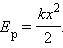
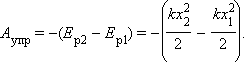
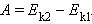
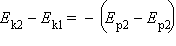 или
или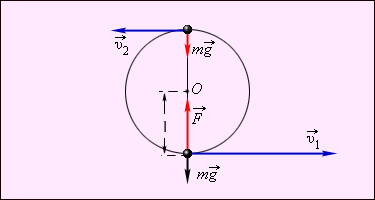
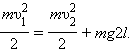
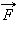 натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.