| Главная » Файлы » Дистанционное обучение » Строители 2 курс |
| [ Скачать с сервера (330.3 Kb) ] | 25.03.2020, 12:50 |
"Построение векторных диаграмм токов и напряжений" Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или по синусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть вектором. Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:
Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их. Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели по расчету электротехнической цепи. При соблюдении всех правил по построению векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:
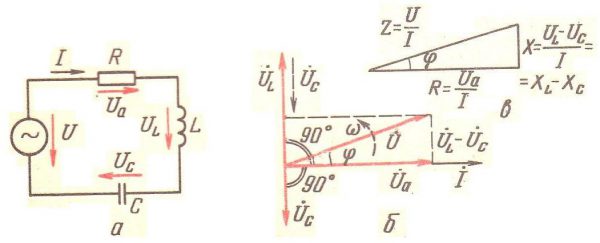
Построение векторной диаграммы напряжений и токов Для лучшего понимания того, как построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь, состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.
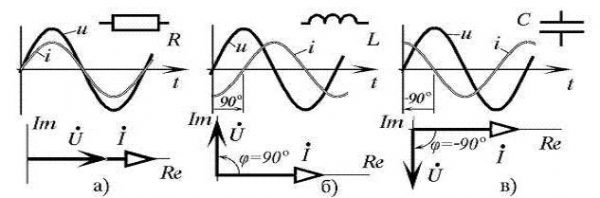
Схема цепи с последовательным соединением элементов Перед тем, как построить векторную диаграмму токов и напряжений, необходимо охарактеризовать все известные параметры цепи. Согласно схемы цепи, изображенной на картинке: U – величина переменного напряжения в текущий момент времени; I – мощность тока в заданный момент времени; UА – напряжение, падающее на активном сопротивлении; UC – напряжение, падающее на емкостной нагрузке; UL – напряжение, падающее на индуктивной нагрузке. Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением: I=Im*cosωt, где: Im – максимальная амплитуда тока; ω – частота тока; t – время. Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно общей величине напряжений на всех элементах цепи: U=UC+UL+UA. В соответствии с законом Ома, падение напряжения на резистивном компоненте равняется: UA= Im*R*cosωt. Противодействие току активного элемента зависит сугубо от свойства проводника и не обуславливается ни характеристиками тока, ни аспектом времени и, соответственно, имеет идентичный с напряжением фазовый сдвиг. Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение:
, где: RC – сопротивление конденсатора; XC – реактивный импеданс конденсатора; C – емкость конденсатора. Реактивное индуктивное сопротивление катушки индуктивности обуславливается наличием изменяющегося по синусоидальному закону электротока, и поскольку напряжение на любом отрезке времени имеет фазовое опережение по отношению к электротоку на π/2, то формула, описывающая колебательный процесс на элементе, выглядит как:
, где: RL – сопротивление катушки индуктивности; XL – реактивный импеданс катушки индуктивности; L – индуктивность катушки. Следовательно, общее напряжение, подведенное к цепи, выглядит: U=Um*cos(ωt±φ), где: Um – максимальная величина напряжения; φ – фазовый сдвиг. Ввиду того, что напряжение и электроток изменяются по синусоидальному закону, и их фиксированные показатели отличаются лишь фазовым сдвигом, то данные величины строятся как вектора. В соответствии с законом сохранения электрического заряда, в любой момент времени сила протекающего тока одинакова, то целесообразно сформировать векторную гистограмму токов.
Векторная диаграмма токов и напряжений RLC цепочке Пусть по оси Х отображается амплитудное значение электротока в цепочке. Поскольку напряжение и электроток на резисторе имеют одинаковый фазовый сдвиг, то вектора данных характеристик будут ориентированы в одну сторону, согласно картинке а. Напряжение на емкостной нагрузке отстает от электрического тока на π/2, и его вектор будет направлен под прямым углом вниз, перпендикулярно напряжению активного сопротивления, согласно картинке в. Напряжение на индуктивной нагрузке опережает электрический ток на π/2, и ее вектор будет ориентирован под прямым углом вверх, перпендикулярно напряжению на активном сопротивлении, согласно картинке б. Для наглядности векторных преобразований пусть UL>UС. Сложив вектора напряжений на реактивных компонентах, получаем, что вектор UL-UС будет направлен перпендикулярно вверх. Суммировав вектора разности напряжений на реактивных компонентах и напряжения на сопротивлении получаем вектор, характеризующий дисперсное значение общего напряжения, согласно картинке 2(б). Аналогично электрическому току, изменяющемуся по синусоидальному закону, напряжение меняется по такому же закону, однако с некоторым фазовым сдвигом. Наблюдается постоянный фазовый сдвиг между напряжением и током. После простых преобразований по постулату Ома, уравнение полного импеданса заданной электрической цепи выглядит как: Z=√R2+(1/ωC- ωL)2. Векторная гистограмма общего и реактивных сопротивлений изображена на картинке 2в. Построение векторных диаграмм токов и напряжений может значительно упростить процесс расчета характеристик контура. Вместе с тем сама процедура позволит наглядно видеть поведение исследуемых характеристик, в зависимости от входных величин. При большом объеме вычислительных операций целесообразно воспользоваться одной из онлайн программ по построению векторных графиков. Если после этого материала остались вопросы, то обязательно посмотрите видео: https://www.youtube.com/watch?v=7au9OB0m92w Домашнее задание:
Отправляете фото или Word-файл с решенной задачей и картой звездного неба на электронный адрес lenr89@mail.ru, не забываем подписать группу и ФИО. | |
| Просмотров: 36 | Загрузок: 11 | | |
| Всего комментариев: 0 | |