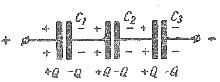"Энергия электрического поля. Электростатическая цепь"

Понятие энергии электрического поля неразрывно связано с понятиями её накопления и расходования. Отсюда следует, что должны быть рассмотрены и накопители этой энергии – электрические конденсаторы. Существенно при этом понимание школьниками, насколько большая энергия может быть сосредоточена в сравнительно небольшом объёме современного конденсатора. Особую значимость имеют эксперименты, показывающие, в каких процессах эта энергия может быть использована для практических нужд.

Энергия плоского конденсатора

Сообщим одной из пластин плоского конденсатора заряд q такой величины, чтобы разность потенциалов между пластинами стала равна U. Если расстояние между пластинами d, то напряжённость электрического поля в конденсаторе Е = U/d.

Одна из пластин конденсатора с зарядом q находится в созданном второй пластиной однородном электрическом поле напряжённостью Е/2, поэтому на неё действует сила притяжения ко второй пластине f = qE/2. Потенциальная энергия заряда q в этом поле равна работе, которую совершает электрическое поле при сближении пластин конденсатора вплотную:

Подставляя в это равенство значение Ed = U и пользуясь формулой, получаем, что энергия электрического поля между пластинами конденсатора:

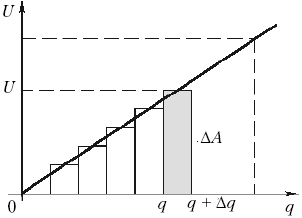
Энергия произвольного конденсатора

Полученная формула справедлива не только для плоского, но и вообще для любого конденсатора. Действительно, напряжение на конденсаторе данной ёмкости прямо пропорционально его заряду U = q/C. Если заряд изменился на малую величину q, то электрическое поле совершило работу А = Uq. Полная работа поля, очевидно, равна площади под графиком:

Ситуация не изменится, если вместо конденсатора использовать уединённый проводник. Его потенциал (относительно бесконечности) равен  = q/С, поэтому энергия электрического поля

Экспериментальное определение энергии, запасённой конденсатором

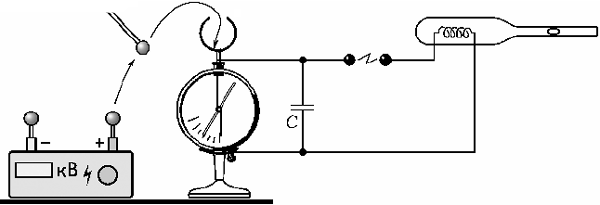
Энергию конденсатора будем измерять по тепловому действию. В пробирке расположим тонкую металлическую спираль. Пробирку закроем пробкой с капиллярной трубкой, внутри которой находится капля воды. Мы получили газовый термометр – прибор, в котором смещение капли в трубке пропорционально количеству теплоты, выделившемуся в пробирке. К спирали через разрядный промежуток из двух металлических шариков подключим конденсатор, параллельно которому подсоединим электрометр с полым шаром. Для заряда конденсатора будем использовать любой источник электричества и металлический шарик на изолирующей ручке.

Зарядим конденсатор до некоторого напряжения и, сблизив шарики, разрядим его через спираль. При этом капля в трубке переместится на определённое расстояние. Так как разряд происходит быстро, то процесс нагревания воздуха в пробирке можно считать адиабатическим, т.е. происходящим без теплообмена с окружающей средой.

Подождём, пока воздух в пробирке охладится, а капля вернётся в исходное положение. Увеличим напряжение в два, а затем в три раза. После разрядов капля переместится на расстояние, соответственно в четыре и девять раз превышающее первоначальное. Заменим конденсатор на другой, ёмкость которого в два раза больше, и зарядим его до исходного напряжения. Тогда при разряде капля переместится в два раза дальше.

Таким образом, опыт подтверждает справедливость формулы W = СU²/2, согласно которой энергия, запасённая в конденсаторе, пропорциональна его ёмкости и квадрату напряжения.

Плотность энергии электрического поля

Выразим энергию электрического поля между обкладками конденсатора такой формулой, чтобы в ней не было величин, характеризующих сам конденсатор, и остались бы только величины, характеризующие поле. Понятно, что этого можно достичь только одним способом: вычислить энергию поля, приходящуюся на единицу объёма. Из формул напряжения на конденсаторе и его емкости, подстановкой этих формул получим:

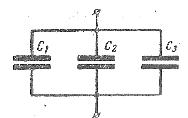
Величина Sd представляет собой объём V электрического поля в конденсаторе. Поэтому плотность энергии электрического поля пропорциональна квадрату его напряжённости.

Параллельное соединение конденсаторов

На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U, Q2 = C2U, Q3 = C3U, а заряд, полученный от источника Q = Q1 + Q2 + Q3. 

Рис. 1. Схема параллельного соединения конденсаторов 

Общая емкость равнозначного (эквивалентного) конденсатора:

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,

т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.

Рис. 2. Способы соединения конденсаторов

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны:  Q1 = Q2 = Q3 = Q

Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.

Рис. 3. Схема последовательного соединения конденсаторов

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов. 

Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.

Домашнее задание:

1. Сделать конспект по данной теме. (присылать его на электронный адрес не нужно)

2. Решить задачи:

• Два заряженных металлических шара приводятся в соприкосновение. Чему будет равен заряд каждого шара после соприкосновения если С1=6мкФ, С2=3мкФ , а потенциалы равны 200 В, и 150 В
• Два конденсатора емкости 2 и 1 мкФ соединены последовательно и присоединены к полюсам батареи с напряжением 120 В. Каково напряжение между обкладками первого и между обкладками второго конденсатора?
• Какой заряд нужно сообщить батарее из двух лейденских банок емкости 0,0005 и 0,001 мкФ, соединенных параллельно, чтобы зарядить ее до напряжения 10 кВ?
• Конденсатор, заряженный до напряжения 100 В, соединяется с конденсатором такой же емкости, но заряженным до 200 В, параллельно (т. е. положительная обкладка – с положительной, отрицательная – с отрицательной). Какое установится напряжение между обкладками?
• Четыре одинаковых конденсатора соединены в одном случае параллельно, в другом – последовательно. В каком случае емкость этой группы конденсаторов больше и во сколько раз?

Отправляете проделанную работу на электронный адрес lenr89@mail.ru, не забываем подписать группу и ФИО.